Page 787 - Capire la matematica

2
3
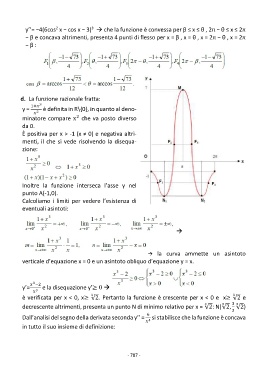
y’’= −4(6cos x − cos x − 3) → che la funzione è convessa per β ≤ x ≤ θ , 2π − θ ≤ x ≤ 2π
− β e concava altrimenti, presenta 4 punti di flesso per x = β , x = θ , x = 2π − θ , x = 2π
− β :

d. La funzione razionale fratta:
1+ 3
y = è definita in R\{0}, in quanto al deno-
2
2
minatore compare x che va posto diverso
da 0.
È positiva per x > -1 (x ≠ 0) e negativa altri-
menti, il che si vede risolvendo la disequa-
zione:

Inoltre la funzione interseca l’asse y nel
punto A(-1,0).
Calcoliamo i limiti per vedere l’esistenza di
eventuali asintoti:

→

→ la curva ammette un asintoto
verticale d’equazione x = 0 e un asintoto obliquo d’equazione y = x.

3
−2
y’= e la disequazione y’≥ 0 →
3
3
3
è verificata per x < 0, x≥ √2. Pertanto la funzione è crescente per x < 0 e x≥ √2 e
3 3
3
3
decrescente altrimenti, presenta un punto N di minimo relativo per x = √2: N(√2, √2)
2
6
Dall’analisi del segno della derivata seconda y’’ = si stabilisce che la funzione è concava
4
in tutto il suo insieme di definizione:

- 787 -